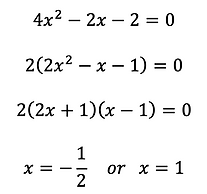Equations involving fractions are rational and are often encountered in calculus. These could be encountered with derivatives and then later
solving derivative equations in maximum and minimum problems. Let's
look at 2 examples of rational equations and solve them.
First, we multiply both sides by 1 - x to get rid of the denominator on the
fraction on the left-side of the equation. The result is:
Simplifying the right-side we have:
Now isolate x:
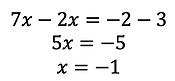
Let's look at an example that involves more than one fraction. This will require that we make a common denominator prior to eliminating it.
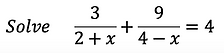
I multiply the first fraction top and bottom by 4-x and the second fraction top and bottom by 2+x. Here is what that step looks like.
Note: I have seen throughout the years many students skip this step and end up doing the problem the wrong way. Please show it.
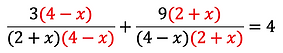
Now that my denominators are the same, I can add and simplify the numerators.
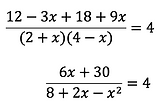
Next, multiply both sides by the denominator of the fraction to eliminate it.
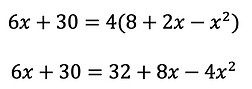
Unlike the previous problem, we cannot isolate x because there are two different exponent on it. The way forward is to move all of the terms to one side (either side is ok), have the equation set to 0,and pick between factoring and the quadratic formula.