Getting comfortable with simplifying expressions involving variables is crucial to understanding advanced calculus. Furthermore, some of the most important expressions you should know are those involving fractions, which we call rational expressions.
1) Addition & Subtraction
Back in elementary school, you learned that you need a "common denominator" to add or
subtract fractions. You can only do so when the bottom of your fractions are identical. The
same principle applies to rational expressions. For instance, say I want to simplify
Here the denominators are two unknowns and are 2 units apart (x - 2 is two units smaller than x). To make them the same, we can multiply them by each other. That's to say the first fraction we will multiply top and bottom by x - 2 and the second fraction top and bottom by x. When applied, this is what you get:
Now that our denominators are the same we could write a single fraction with x(x-2) as the
denominator and simplify the result for the numerator as follows:
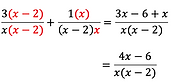
2) Multiplication
Unfortunately, the way you learned multiplication of fractions in elementary school is not as
practical for advanced math. You most likely were taught to "multiply across", which is to say multiply the numerators and multiply the denominators. After that, you reduce your fraction to its simplest form. That
approach will not work with advanced rational expressions. Instead, we are going to "cross-cancel" the common factors and then "multiply across". Here is a simple example.
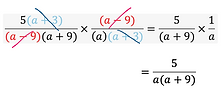
You may have noticed that the example above is written in factored form. If that's not the case, you need to factor your fractions and then apply cancellations. Let's look at an example.

Here it looks like I cannot cancel anything, but rewriting each of the components in factored form yields
Applying cross-cancellations, we get:
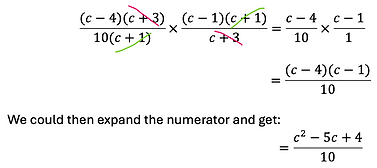
3) Division
When we divide fractions, we "flip the second one and multiply them". That rule also applies to rational expressions along with cross-cancellations. Here is an example to illustrate this process.
